| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 5.1 | Exercise 5.2 | |
Chapter 5 Lines and Angles
Welcome to the solutions guide for Chapter 5, "Lines and Angles," a fundamental chapter in geometry presented within the latest Class 7 NCERT mathematics textbook for the academic session 2024-25. Building upon the foundational concepts introduced in earlier classes, this chapter delves deeper into the intricate relationships between lines and the angles they form when they intersect or are intersected by other lines. Mastering these relationships is crucial for developing spatial reasoning and is a cornerstone for all future studies in geometry. These solutions offer detailed explanations and clear, step-by-step methods to navigate the exercises successfully.
A significant portion of this chapter, and consequently these solutions, revolves around understanding various pairs of angles and their specific properties. The solutions provide precise definitions, illustrative diagrams, and worked examples for identifying and utilizing the relationships between:
- Complementary Angles: Two angles whose measures add up to exactly $90^\circ$. If one angle is $x$, its complement is $90^\circ - x$.
- Supplementary Angles: Two angles whose measures sum to precisely $180^\circ$. If one angle is $y$, its supplement is $180^\circ - y$.
- Adjacent Angles: Two angles that share a common vertex and a common arm (side), but do not overlap in their interiors.
- Linear Pair: A special pair of adjacent angles whose non-common arms form a straight line. Angles in a linear pair are always supplementary, summing to $180^\circ$.
- Vertically Opposite Angles: The angles formed opposite each other when two lines intersect. A key property, demonstrated in the solutions, is that vertically opposite angles are always equal in measure.
The chapter then progresses to a crucial scenario in geometry: a line, known as a transversal, intersecting two other lines. The solutions focus particularly on the special case where the two lines intersected by the transversal are parallel. When parallel lines are cut by a transversal, specific pairs of angles are formed that have predictable and useful relationships. The solutions meticulously identify, explain, and utilize the properties of:
- Corresponding Angles: Angles in the same relative position at each intersection where the transversal intersects the two lines. When lines are parallel, corresponding angles are equal.
- Alternate Interior Angles: Angles that lie between the two lines and on opposite sides of the transversal. When lines are parallel, alternate interior angles are equal.
- Alternate Exterior Angles: Angles that lie outside the two lines and on opposite sides of the transversal. When lines are parallel, alternate exterior angles are equal.
- Consecutive Interior Angles (or Co-interior Angles): Angles that lie between the two lines but on the same side of the transversal. When lines are parallel, consecutive interior angles are supplementary (their sum is $180^\circ$).
The power of these properties lies in their application. The solutions demonstrate extensively how to use the equality or supplementary nature of these angle pairs to deduce the measures of unknown angles in geometric figures, given that lines are parallel or, conversely, to determine if two lines are parallel based on the angles formed by a transversal. Diagrams are used heavily throughout the solutions to visually clarify the positions of these angle pairs and the logic applied in solving problems. Logical deduction, starting from known facts (like parallel lines) and applying established properties, is central to the problem-solving approach shown.
Regarding the rationalized syllabus for 2024-25, Chapter 5, "Lines and Angles," in the Class 7 NCERT textbook retains its strong focus on the core concepts of angle pairs, transversals, and the properties of angles formed when a transversal intersects parallel lines. The rationalization process mainly involved streamlining the number and types of exercises, ensuring students master these fundamental geometric relationships without excessive complexity. The critical definitions and properties related to parallel lines and angles remain central to the curriculum. By carefully studying these comprehensive solutions, students can solidify their understanding of angle terminology and relationships, master the application of geometric properties to find missing angle measures, and significantly develop the deductive reasoning skills essential for success in geometry and beyond.
Exercise 5.1
Question 1. Find the complement of each of the following angles:

Answer:
Solution:
Two angles are said to be complementary if the sum of their measures is $90^\circ$.
The complement of an angle with measure $x^\circ$ is $(90 - x)^\circ$.
(i) The given angle is $20^\circ$.
The complement of $20^\circ$ is $(90 - 20)^\circ = 70^\circ$.
$\text{Complement} = 90^\circ - 20^\circ = 70^\circ$
(ii) The given angle is $63^\circ$.
The complement of $63^\circ$ is $(90 - 63)^\circ = 27^\circ$.
$\text{Complement} = 90^\circ - 63^\circ = 27^\circ$
(iii) The given angle is $57^\circ$.
The complement of $57^\circ$ is $(90 - 57)^\circ = 33^\circ$.
$\text{Complement} = 90^\circ - 57^\circ = 33^\circ$
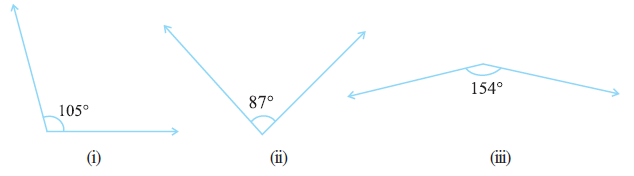
Question 2. Find the supplement of each of the following angles:
Answer:
Solution:
Two angles are said to be supplementary if the sum of their measures is $180^\circ$.
The supplement of an angle with measure $x^\circ$ is $(180 - x)^\circ$.
(i) The given angle is $105^\circ$.
The supplement of $105^\circ$ is $(180 - 105)^\circ = 75^\circ$.
$\text{Supplement} = 180^\circ - 105^\circ = 75^\circ$
(ii) The given angle is $87^\circ$.
The supplement of $87^\circ$ is $(180 - 87)^\circ = 93^\circ$.
$\text{Supplement} = 180^\circ - 87^\circ = 93^\circ$
(iii) The given angle is $154^\circ$.
The supplement of $154^\circ$ is $(180 - 154)^\circ = 26^\circ$.
$\text{Supplement} = 180^\circ - 154^\circ = 26^\circ$
Question 3. Identify which of the following pairs of angles are complementary and which are supplementary.
(i) 65º, 115º
(ii) 63º, 27º
(iii) 112º, 68º
(iv) 130º, 50º
(v) 45º, 45º
(vi) 80º, 10º
Answer:
Solution:
Two angles are complementary if their sum is $90^\circ$.
Two angles are supplementary if their sum is $180^\circ$.
(i) 65º, 115º
Sum of angles $= 65^\circ + 115^\circ = 180^\circ$.
Since the sum is $180^\circ$, the pair of angles is supplementary.
(ii) 63º, 27º
Sum of angles $= 63^\circ + 27^\circ = 90^\circ$.
Since the sum is $90^\circ$, the pair of angles is complementary.
(iii) 112º, 68º
Sum of angles $= 112^\circ + 68^\circ = 180^\circ$.
Since the sum is $180^\circ$, the pair of angles is supplementary.
(iv) 130º, 50º
Sum of angles $= 130^\circ + 50^\circ = 180^\circ$.
Since the sum is $180^\circ$, the pair of angles is supplementary.
(v) 45º, 45º
Sum of angles $= 45^\circ + 45^\circ = 90^\circ$.
Since the sum is $90^\circ$, the pair of angles is complementary.
(vi) 80º, 10º
Sum of angles $= 80^\circ + 10^\circ = 90^\circ$.
Since the sum is $90^\circ$, the pair of angles is complementary.
Question 4. Find the angle which is equal to its complement.
Answer:
Solution:
To Find:
The angle which is equal to its complement.
Let:
Let the angle be $x^\circ$.
Concept:
The complement of an angle $x^\circ$ is $(90 - x)^\circ$.
According to the problem, the angle is equal to its complement.
Equation:
So, we can write the equation:
$x = 90 - x$
Solve:
To solve for $x$, add $x$ to both sides of the equation:
$x + x = 90 - x + x$
$2x = 90$
Now, divide both sides by 2:
$\frac{2x}{2} = \frac{90}{2}$
$x = 45$
The angle is $45^\circ$. Its complement is $(90 - 45)^\circ = 45^\circ$. The angle is indeed equal to its complement.
Answer:
The angle which is equal to its complement is $\mathbf{45^\circ}$.
Question 5. Find the angle which is equal to its supplement.
Answer:
Solution:
To Find:
The angle which is equal to its supplement.
Let:
Let the angle be $x^\circ$.
Concept:
The supplement of an angle $x^\circ$ is $(180 - x)^\circ$.
According to the problem, the angle is equal to its supplement.
Equation:
So, we can write the equation:
$x = 180 - x$
Solve:
To solve for $x$, add $x$ to both sides of the equation:
$x + x = 180 - x + x$
$2x = 180$
Now, divide both sides by 2:
$\frac{2x}{2} = \frac{180}{2}$
$x = 90$
The angle is $90^\circ$. Its supplement is $(180 - 90)^\circ = 90^\circ$. The angle is indeed equal to its supplement.
Answer:
The angle which is equal to its supplement is $\mathbf{90^\circ}$.
Question 6. In the given figure, ∠1 and ∠2 are supplementary angles.

If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary.
Answer:
Solution:
Given that $\angle 1$ and $\angle 2$ are supplementary angles.
This means that the sum of their measures is $180^\circ$.
$\angle 1 + \angle 2 = 180^\circ$
If $\angle 1$ is decreased, for the sum of the two angles to remain $180^\circ$, $\angle 2$ must change.
Let's consider an example.
Suppose $\angle 1 = 100^\circ$ and $\angle 2 = 80^\circ$. Their sum is $100^\circ + 80^\circ = 180^\circ$, so they are supplementary.
Now, let's decrease $\angle 1$ by $10^\circ$. The new $\angle 1$ becomes $100^\circ - 10^\circ = 90^\circ$. The amount of decrease is $10^\circ$.
For the angles to remain supplementary, the new $\angle 1$ and the new $\angle 2$ must still add up to $180^\circ$.
$90^\circ + \text{New } \angle 2 = 180^\circ$.
This means the New $\angle 2 = 180^\circ - 90^\circ = 90^\circ$.
The original $\angle 2$ was $80^\circ$, and the new $\angle 2$ is $90^\circ$.
The change in $\angle 2$ is $90^\circ - 80^\circ = 10^\circ$. This is an increase.
We decreased $\angle 1$ by $10^\circ$ and $\angle 2$ increased by $10^\circ$. The amount of decrease in $\angle 1$ is equal to the amount of increase in $\angle 2$.
Therefore, if $\angle 1$ is decreased by some amount, $\angle 2$ must be increased by the same amount so that both the angles still remain supplementary.
Question 7. Can two angles be supplementary if both of them are:
(i) acute?
(ii) obtuse?
(iii) right?
Answer:
Solution:
Two angles are supplementary if the sum of their measures is $180^\circ$.
(i) acute?
An acute angle has a measure less than $90^\circ$.
If we take two acute angles, the measure of each angle is less than $90^\circ$.
The sum of two acute angles will be less than $90^\circ + 90^\circ$.
Sum of two acute angles $< 180^\circ$.
Since the sum is less than $180^\circ$, two acute angles cannot be supplementary.
Answer: No
(ii) obtuse?
An obtuse angle has a measure greater than $90^\circ$.
If we take two obtuse angles, the measure of each angle is greater than $90^\circ$.
The sum of two obtuse angles will be greater than $90^\circ + 90^\circ$.
Sum of two obtuse angles $> 180^\circ$.
Since the sum is greater than $180^\circ$, two obtuse angles cannot be supplementary.
Answer: No
(iii) right?
A right angle has a measure exactly equal to $90^\circ$.
If we take two right angles, the measure of each angle is exactly $90^\circ$.
The sum of two right angles is $90^\circ + 90^\circ$.
Sum of two right angles $= 180^\circ$.
Since the sum is exactly $180^\circ$, two right angles can be supplementary.
Answer: Yes
Question 8. An angle is greater than 45º. Is its complementary angle greater than 45º or equal to 45º or less than 45º?
Answer:
Solution:
Two angles are complementary if the sum of their measures is $90^\circ$.
Let the given angle be Angle 1 and its complementary angle be Angle 2.
We know that:
Angle 1 + Angle 2 = $90^\circ$
We are given that Angle 1 is greater than $45^\circ$.
Angle 1 $> 45^\circ$
Since Angle 1 is greater than $45^\circ$, it means that Angle 1 takes up more than half of the total sum of $90^\circ$.
For example, if Angle 1 was exactly $45^\circ$, then Angle 2 would be $90^\circ - 45^\circ = 45^\circ$.
If Angle 1 is greater than $45^\circ$ (like $50^\circ$, $60^\circ$, etc.), then Angle 2 must be smaller than $45^\circ$ to make the sum $90^\circ$.
Let's check with an example:
Suppose Angle 1 = $50^\circ$. This is greater than $45^\circ$.
Angle 1 + Angle 2 = $90^\circ$
$50^\circ$ + Angle 2 = $90^\circ$
Angle 2 = $90^\circ - 50^\circ$
Angle 2 = $40^\circ$
$40^\circ$ is less than $45^\circ$.
So, if an angle is greater than $45^\circ$, its complementary angle must be the remaining part to reach $90^\circ$. This remaining part will be less than $45^\circ$.
Therefore, if an angle is greater than $45^\circ$, its complementary angle is less than 45º.
Question 9. Fill in the blanks:
(i) If two angles are complementary, then the sum of their measures is _______.
(ii) If two angles are supplementary, then the sum of their measures is ______.
(iii) If two adjacent angles are supplementary, they form a ___________.
Answer:
Solution:
Let's fill in the blanks based on the definitions of complementary and supplementary angles, and the property of adjacent angles.
(i) If two angles are complementary, then the sum of their measures is $\underline{\mathbf{90^\circ}}$.
(ii) If two angles are supplementary, then the sum of their measures is $\underline{\mathbf{180^\circ}}$.
(iii) If two adjacent angles are supplementary, they form a $\underline{\text{linear pair}}$.
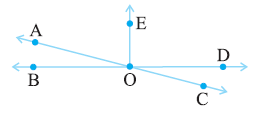
Question 10. In the adjoining figure, name the following pairs of angles.
(i) Obtuse vertically opposite angles
(ii) Adjacent complementary angles
(iii) Equal supplementary angles
(iv) Unequal supplementary angles
(v) Adjacent angles that do not form a linear pair
Answer:
Solution:
Lines AC and BD intersect at point O.
$\angle$AOD is an obtuse angle.
Ray OE is perpendicular to line BD, and it is drawn between $\angle$AOD.
(i) Obtuse vertically opposite angles
Vertically opposite angles are formed by two intersecting lines. They are opposite to each other at the vertex and are equal.
The intersecting lines are AC and BD. The pairs of vertically opposite angles are ($\angle$AOD, $\angle$BOC) and ($\angle$AOB, $\angle$DOC).
We are given that $\angle$AOD is obtuse. Since $\angle$BOC is vertically opposite to $\angle$AOD, $\angle$BOC is also obtuse.
$\angle$AOB and $\angle$DOC are vertically opposite. Since $\angle$AOD and $\angle$AOB form a linear pair on line BD ($\angle$AOD + $\angle$AOB = $180^\circ$), and $\angle$AOD is obtuse ($> 90^\circ$), $\angle$AOB must be acute ($< 90^\circ$). Similarly, $\angle$DOC is acute.
Therefore, the obtuse vertically opposite angles are ($\angle$AOD, $\angle$BOC).
(ii) Adjacent complementary angles
Adjacent angles share a common vertex and a common arm. Complementary angles are two angles whose sum is $90^\circ$.
We are given that ray OE is perpendicular to line BD. This means that the angle formed by OE and BD is $90^\circ$. Thus, $\angle$EOB = $90^\circ$.
The angle $\angle$EOB is formed by the adjacent angles $\angle$EOA and $\angle$AOB. They share the common vertex O and the common arm OA.
The sum of these adjacent angles is $\angle$EOA + $\angle$AOB = $\angle$EOB.
$\angle$EOA + $\angle$AOB = $90^\circ$
Since their sum is $90^\circ$, $\angle$EOA and $\angle$AOB are complementary.
Therefore, the adjacent complementary angles are ($\angle$EOA, $\angle$AOB).
(iii) Equal supplementary angles
Supplementary angles are two angles whose sum is $180^\circ$. Equal supplementary angles must each measure $180^\circ / 2 = 90^\circ$.
We know that OE is perpendicular to line BD. This implies $\angle$EOB = $90^\circ$ and $\angle$EOD = $90^\circ$.
These two angles, $\angle$EOB and $\angle$EOD, share the common vertex O and the common arm OE. Their non-common arms OB and OD form the straight line BD. Thus, they are adjacent and form a linear pair.
$\angle$EOB = $90^\circ$
[Given OE $\perp$ BD]
$\angle$EOD = $90^\circ$
[Given OE $\perp$ BD]
Since $\angle$EOB = $\angle$EOD = $90^\circ$, they are equal.
Their sum is $\angle$EOB + $\angle$EOD = $90^\circ + 90^\circ = 180^\circ$, so they are supplementary.
Therefore, the equal supplementary angles are ($\angle$EOB, $\angle$EOD).
(iv) Unequal supplementary angles
Supplementary angles are two angles whose sum is $180^\circ$. Unequal supplementary angles add up to $180^\circ$ but have different measures.
Consider the angles $\angle$EOA and $\angle$EOC. They are adjacent angles sharing the common vertex O and the common arm OE. Their non-common arms OA and OC form the straight line AC.
Thus, $\angle$EOA and $\angle$EOC form a linear pair, so their sum is $180^\circ$. They are supplementary.
$\angle$EOA + $\angle$EOC = $180^\circ$
[Linear Pair on line AC]
Since, $\angle$EOA is acute (from figure/deduction if $\angle$AOD is obtuse) and $\angle$EOC is obtuse. Therefore, $\angle$EOA $\neq \angle$EOC.
Thus, the unequal supplementary angles are ($\angle$EOA, $\angle$EOC).
(v) Adjacent angles that do not form a linear pair
Adjacent angles share a common vertex and a common arm. A linear pair is a special case of adjacent angles where the non-common arms form a straight line, and their sum is $180^\circ$. We need adjacent angles whose non-common arms do not form a straight line (i.e., their sum is not $180^\circ$).
Let's look at the given pairs:
($\angle$AOB, $\angle$AOE): These angles are adjacent (common vertex O, common arm OA). Their sum is $\angle$AOB + $\angle$AOE = $\angle$EOB. We know $\angle$EOB = $90^\circ$. Since $90^\circ \neq 180^\circ$, they do not form a linear pair.
($\angle$AOE, $\angle$EOD): These angles are adjacent (common vertex O, common arm OE). Their sum is $\angle$AOE + $\angle$EOD = $\angle$AOD. We are given that $\angle$AOD is obtuse. Since an obtuse angle is $> 90^\circ$ and not $180^\circ$ (unless it's a straight angle, which $\angle$AOD is not, as AC is a straight line), $\angle$AOD is not $180^\circ$. So, they do not form a linear pair.
($\angle$EOD, $\angle$COD): These angles are adjacent (common vertex O, common arm OD). Their sum is $\angle$EOD + $\angle$COD = $\angle$EOC. As shown in part (iv), $\angle$EOC is obtuse ($> 90^\circ$) and not $180^\circ$. So, they do not form a linear pair.
All three pairs are adjacent and do not form a linear pair.
Therefore, adjacent angles that do not form a linear pair are ($\angle$AOB, $\angle$AOE); ($\angle$AOE, $\angle$EOD); ($\angle$EOD, $\angle$COD).
Exercise 5.2
Question 1. State the property that is used in each of the following statements?
(i) If a || b, then ∠1 = ∠5.
(ii) If ∠4 = ∠6, then a || b.
(iii) If ∠4 + ∠5 = 180°, then a || b

Answer:
Solution:
We need to identify the property that relates the angles when two lines are intersected by a transversal.
(i) If a || b, then $\angle 1 = \angle 5$.
In the given figure, $\angle 1$ and $\angle 5$ are in corresponding positions (upper left corner at each intersection point).
The property used is the Corresponding Angles Property.
This property states that if two parallel lines are intersected by a transversal, then each pair of corresponding angles is equal.
(ii) If $\angle 4 = \angle 6$, then a || b.
In the given figure, $\angle 4$ and $\angle 6$ are interior angles on opposite sides of the transversal.
The property used is the Alternate Interior Angles Property.
This property (or its converse) states that if a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
(iii) If $\angle 4 + \angle 5 = 180^\circ$, then a || b.
In the given figure, $\angle 4$ and $\angle 5$ are interior angles on the same side of the transversal.
The property used is the Consecutive Interior Angles Property (or Interior Angles on the Same Side of the Transversal Property).
This property (or its converse) states that if a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary (their sum is $180^\circ$), then the two lines are parallel.
Question 2. In the adjoining figure, identify
(i) the pairs of corresponding angles.
(ii) the pairs of alternate interior angles.
(iii) the pairs of interior angles on the same side of the transversal.
(iv) the vertically opposite angles.

Answer:
Solution:
In the given figure, lines 'a' and 'b' are intersected by the transversal line 'c'. Let's identify the different pairs of angles formed.
(i) The pairs of corresponding angles.
Corresponding angles are angles that are in the same relative position at each intersection where a straight line crosses two others.
The pairs of corresponding angles are:
($\angle 1, \angle 5$); ($\angle 2, \angle 6$); ($\angle 3, \angle 7$); ($\angle 4, \angle 8$)
(ii) The pairs of alternate interior angles.
Alternate interior angles are interior angles on opposite sides of the transversal.
The pairs of alternate interior angles are:
($\angle 2, \angle 8$); ($\angle 3, \angle 5$)
(iii) The pairs of interior angles on the same side of the transversal.
These are interior angles on the same side of the transversal.
The pairs of interior angles on the same side of the transversal are:
($\angle 2, \angle 5$); ($\angle 3, \angle 8$)
(iv) The vertically opposite angles.
Vertically opposite angles are formed by two intersecting lines and are opposite to each other at the point of intersection. They are always equal.
At the intersection of lines 'a' and 'c', the pairs are:
($\angle 1, \angle 3$); ($\angle 2, \angle 4$)
At the intersection of lines 'b' and 'c', the pairs are:
($\angle 5, \angle 7$); ($\angle 6, \angle 8$)
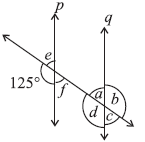
Question 3. In the adjoining figure, p || q. Find the unknown angles.
Answer:
Solution:
Given that lines p and q are parallel (p || q), and they are intersected by a transversal line.
We are given one angle measuring $125^\circ$ at the intersection with line p. We need to find the measures of the angles labelled a, b, c, d, e, and f.
Since p || q, we can use the properties of angles formed by a transversal intersecting parallel lines.
By observing the figure and using the property of corresponding angles:
$\angle d = 125^\circ$
(Corresponding angles)
Now, let's consider the angles at the intersection of line p with the transversal.
Angle $\angle e$ and the $125^\circ$ angle are adjacent angles on the straight line p. They form a linear pair, so their sum is $180^\circ$.
$\angle e + 125^\circ = 180^\circ$
(Linear pair)
Subtracting $125^\circ$ from both sides:
$\angle e = 180^\circ - 125^\circ$
... (i)
$\angle e = 55^\circ$
From the rule of vertically opposite angles at the intersection with line p:
$\angle f = \angle e$
(Vertically opposite angles)
Since $\angle e = 55^\circ$ (from i),
$\angle f = 55^\circ$
From the rule of vertically opposite angles at the intersection with line q:
$\angle b = \angle d$
(Vertically opposite angles)
Since $\angle d = 125^\circ$,
$\angle b = 125^\circ$
By the property of corresponding angles, relating angles at line q and line p:
$\angle c = \angle f$
(Corresponding angles, p || q)
Since $\angle f = 55^\circ$,
$\angle c = 55^\circ$
By the property of corresponding angles, relating angles at line q and line p:
$\angle a = \angle e$
(Corresponding angles, p || q)
Since $\angle e = 55^\circ$,
$\angle a = 55^\circ$
The unknown angles are:
$\angle a = 55^\circ$
$\angle b = 125^\circ$
$\angle c = 55^\circ$
$\angle d = 125^\circ$
$\angle e = 55^\circ$
$\angle f = 55^\circ$
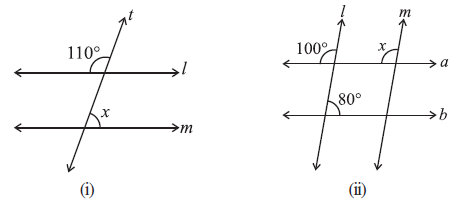
Question 4. Find the value of x in each of the following figures if l || m.
Answer:
Solution:
(i) Figure 1:
Given that line l is parallel to line m (l || m), and they are intersected by a transversal.
We are given one angle is $110^\circ$ and the angle $\angle$x. We need to find the value of x.
Let us assume the angle adjacent to $\angle$x on the line m is $\angle$y, such that $\angle$y is above line m and on the left side of the transversal. This angle $\angle$y is in the same position relative to line m and the transversal as the $110^\circ$ angle is relative to line l and the transversal.
By the property of corresponding angles, since l || m, the corresponding angles are equal.
$\angle y = 110^\circ$
(Corresponding angles, l || m)
We know that a linear pair is a pair of adjacent angles whose non-common arms form a straight line, and their sum is $180^\circ$.
Angles $\angle$x and $\angle$y are adjacent angles on the straight line m. They form a linear pair.
$\angle x + \angle y = 180^\circ$
(Linear pair)
Substitute the value of $\angle y$ into the equation:
$\angle x + 110^\circ = 180^\circ$
... (i)
Subtract $110^\circ$ from both sides of the equation:
$\angle x = 180^\circ - 110^\circ$
$\angle x = 70^\circ$
The value of x is $70^\circ$.
(ii) Figure 2:
Given that line l is parallel to line m (l || m), and they are intersected by a transversal.
We are given one exterior angle is $100^\circ$ and one interior angle is $\angle$x. We need to find the value of x.
By the property of corresponding angles, since l || m, the corresponding angles are equal.
Angle $\angle$x is in the interior, below line m, on the right side of the transversal.
The angle $100^\circ$ is in the exterior, above line l, on the right side of the transversal.
These two angles are in corresponding positions.
$\angle x = 100^\circ$
(Corresponding angles, l || m)
The value of x is $100^\circ$.
Question 5. In the given figure, the arms of two angles are parallel.
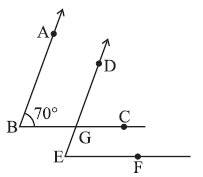
If ∠ABC = 70º, then find
(i) ∠DGC
(ii) ∠DEF
Answer:
Given:
In the given figure, the arms of two angles, $\angle$ABC and $\angle$DEF, are parallel.
This means AB $\parallel$ DE and BC $\parallel$ EF.
We are also given that $\angle$ABC = $70^\circ$.
To Find:
(i) $\angle$DGC
(ii) $\angle$DEF
Solution:
(i) Finding $\angle$DGC:
Consider the parallel lines AB and DE and the transversal BC.
AB $\parallel$ DE
(Given)
When a transversal intersects two parallel lines, the corresponding angles are equal.
In this case, $\angle$ABC and $\angle$DGC are corresponding angles.
$\angle$DGC = $\angle$ABC
(Corresponding angles)
$\angle$ABC = $70^\circ$
(Given)
Therefore,
$\angle$DGC = $70^\circ$
(ii) Finding $\angle$DEF:
Now consider the parallel lines BC and EF and the transversal DE.
BC $\parallel$ EF
(Given)
When a transversal intersects two parallel lines, the corresponding angles are equal.
In this case, $\angle$DGC and $\angle$DEF are corresponding angles.
$\angle$DEF = $\angle$DGC
(Corresponding angles)
From part (i), we found that $\angle$DGC = $70^\circ$.
Therefore,
$\angle$DEF = $70^\circ$
Answer:
(i) $\angle$DGC = $70^\circ$
(ii) $\angle$DEF = $70^\circ$
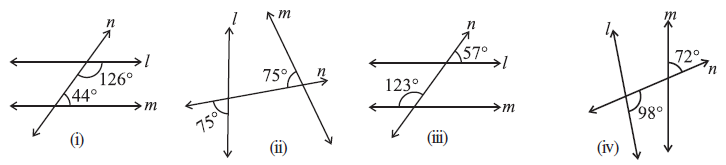
Question 6. In the given figures below, decide whether l is parallel to m.
Answer:
We need to determine if line l is parallel to line m in each figure based on the given angle measures.
We will use the properties of angles formed by a transversal intersecting two lines:
- If corresponding angles are equal, the lines are parallel.
- If alternate interior angles are equal, the lines are parallel.
- If consecutive interior angles are supplementary (sum is $180^\circ$), the lines are parallel.
Solution:
(i) Figure 1:
Let us consider the two lines, l and m.
The transversal line intersects l and m.
The angles given are $126^\circ$ and $44^\circ$. These are interior angles on the same side of the transversal.
We know that if the sum of interior angles on the same side of the transversal is $180^\circ$, then the lines are parallel.
Let's find the sum of the given interior angles:
$126^\circ + 44^\circ = 170^\circ$
The sum of interior angles on the same side of the transversal is $170^\circ$.
Since the sum is not equal to $180^\circ$, line l is not parallel to line m.
(ii) Figure 2:
Let us consider the two lines, l and m.
The transversal line intersects l and m.
Let us assume $\angle$x be the vertically opposite angle formed due to the intersection of the straight line l and transversal. This angle is below line l and to the right of the transversal. The given $75^\circ$ angle is above line l and to the right.
So, $\angle$x $= 75^\circ$ (Vertically opposite angles).
We know that if the sum of interior angles on the same side of the transversal is $180^\circ$, then the lines are parallel.
The interior angles on the same side of the transversal are the angle $\angle$x (below l, right) and the interior angle below line m, right. The given $75^\circ$ is above line m, right. The interior angle below line m, right forms a linear pair with the angle above line m, right if that angle was $75^\circ$.
Let's consider the given angles. One is above line l, right ($75^\circ$). The other is above line m, right ($75^\circ$). These are corresponding angles.
If corresponding angles are equal, lines are parallel. In this figure, corresponding angles are equal ($75^\circ = 75^\circ$).
Thus, line l is parallel to line m.
(iii) Figure 3:
Let us consider the two lines, l and m. The transversal line intersects l and m.
Let us assume $\angle$x be the vertically opposite angle formed due to the intersection of the Straight line l and transversal line n. This angle is above line l and to the right of the transversal.
We know that the sum of interior angles on the same side of the transversal is $180^\circ$ if the lines are parallel.
The provided solution calculates the sum of the given angles ($123^\circ$ and $57^\circ$):
$123^\circ + \angle x = 123^\circ + 57^\circ = 180^\circ$
The sum of these two angles is $180^\circ$.
Therefore, the sum of interior angles on the same side of the transversal is equal to $180^\circ$.
So, line l is parallel to line m.
(iv) Figure 4:
Let us consider the two lines, l and m.
The transversal line intersects l and m.
The angles given are $98^\circ$ and $72^\circ$. These are interior angles on the same side of the transversal.
We know that if the sum of interior angles on the same side of the transversal is $180^\circ$, then the lines are parallel.
Let's find the sum of the given interior angles:
$98^\circ + 72^\circ = 170^\circ$
The sum of interior angles on the same side of the transversal is $170^\circ$.
Since the sum is not equal to $180^\circ$, line l is not parallel to line m.

